在同一市场上销售两种性能有差异的同一类手机A与B，设Q_A，Q_B分别表示它们的需求量，P_A，P_B分别为其价格，生产这两种手机每部所需平均成本分别为

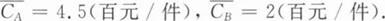
已知需求函数分别为
Q_A=9.5-P_A+2P_B，Q_B=7+2P_A-5P_B，
试确定其价格，使其利润最大．

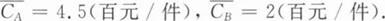
依题设，总利润函数为：
π = (Q_A × P_A) + (Q_B × P_B) - C_A × Q_A - C_B × Q_B，其中，C_A、C_B分别为生产这两种手机每部所需平均成本。
根据需求函数 Q_A 和 Q_B 分别代入利润函数中，得到：
π = (9.5 - P_A + 2P_B) × P_A + (7 + 2P_A - 5P_B) × P_B - C_A × (9.5 - P_A + 2P_B) - C_B × (7 + 2P_A - 5P_B)。
为了确定使利润最大的价格，需要对利润函数进行微分，并令其为零，解出 P_A 和 P_B 的值。这些值代表了使利润最大的价格。具体计算过程较为复杂，需要用到微积分的知识。