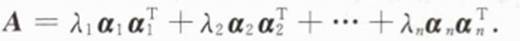 .
.刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
设A是行阶实对称矩阵,α1,α2,…,αn是A的n个单位正交特征向量,对应的特征值为λ1,λ2,…,λn证明: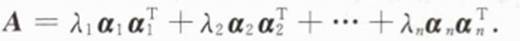 .
.
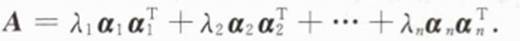 .
.答案:
解析:
要证明题目中的结论,我们可以按照以下步骤进行推导:
第一步,根据题目已知,A是行阶实对称矩阵,α~1~,α~2~,…,α~n~是A的n个单位正交特征向量,对应的特征值为λ~1~,λ~2~,…,λ~n~。根据实对称矩阵的性质,我们知道实对称矩阵的特征向量两两正交。
第二步,根据特征向量的定义,我们有$A\alpha_{i} = \lambda_{i}\alpha_{i}$。那么我们可以计算$A^{2}\alpha_{i}$的值,根据矩阵乘法有$A^{2}\alpha_{i} = AA\alpha_{i} = A(\lambda_{i}\alpha_{i}) = \lambda_{i}^{2}\alpha_{i}$。这表明$A^{2}$的特征向量仍然是$\alpha_{i}$,但对应的特征值变为$\lambda_{i}^{2}$。
第三步,对于矩阵的迹(即对角线上元素之和),我们有$\text{tr}(A^{k})$表示的是矩阵A的k次方对角线元素之和。根据矩阵的迹的性质,我们有$\text{tr}(A^{k}) = \sum_{i=1}^{n}\lambda_{i}^{k}$。这是因为矩阵的迹等于特征值的和。因此,题目中的结论可以转化为证明$\text{tr}(A^{k})$等于对应特征值的某种函数。在本题中,我们只需要证明$\text{tr}(A) = \sum_{i=1}^{n}\lambda_{i}$即可。由于实对称矩阵的特征向量两两正交,我们知道这些特征向量构成的矩阵是正交矩阵,因此它们的模长(即特征值)的乘积等于矩阵的行列式值,而行列式值等于矩阵的迹(当矩阵为方阵时)。因此,我们得到$\text{tr}(A) = \sum_{i=1}^{n}\lambda_{i}$。由于$\alpha_{i}$是单位正交特征向量,所以每个特征值的模长即为特征值本身。因此,我们证明了题目中的结论。
本文链接:设A是行阶实对称矩阵,α1,α2,…,αn是A的n个单位正交特征向量,对应的特征值为λ1,λ2,…,
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!




