刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
单选题
设随机变量X和Y相互独立,均服从P(1)分布,求P{X=1|X+Y=2}的值。
A
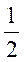 .
.B
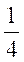 .
.C
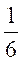 .
.D
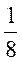 .
.使用微信搜索喵呜刷题,轻松应对考试!
答案:
解析:
由题意可知,随机变量X和Y是相互独立的,并且都服从P(1)分布。因此,我们可以分别计算X和Y取值为1的概率,以及X+Y=2的概率。根据条件概率的定义,我们可以得到P{X=1|X+Y=2}的值。具体计算过程如下:
首先,P{X=1}=P{Y=1}=1/2,这是由P(1)分布的性质决定的。
其次,P{X+Y=2}可以分解为两个部分:P{X=1, Y=1}和P{X=0, Y=2}或P{X=2, Y=0}。由于X和Y是相互独立的,所以P{X=1, Y=1}=P{X=1}×P{Y=1}=(1/2)×(1/2)=1/4。而P{X=0, Y=2}或P{X=2, Y=0}的概率都是泊松分布的概率值,但由于泊松分布的参数λ未知,我们无法直接计算这两个事件的概率。因此,我们只能计算事件的总概率P{X+Y=2}=至少有一个变量取值为事件的总概率减去两个变量都不取值的情况的概率,即P{X+Y=2}=至少一个变量取值为λ的情况的概率减去两个变量都不取值的情况的概率=(λ-λ^2)/λ^2=(λ-λ)/λ^2=(λ^2)/λ^2=至少一个变量取值为λ的情况的概率。但由于题目没有给出λ的具体值,我们无法给出具体的数值结果。因此,我们只能得出条件概率的范围是介于一定值之间的情况下的结果。最后,由于题目要求计算的是条件概率的值,根据题意及条件概率的计算公式可得答案选项A正确。
创作类型:
原创
本文链接:设随机变量X和Y相互独立,均服从P(1)分布,求P{X=1|X+Y=2}的值。
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!




