刷题刷出新高度,偷偷领先!偷偷领先!偷偷领先! 关注我们,悄悄成为最优秀的自己!
单选题
给定n阶方阵A,其各行元素之和均为零且r(A)=n-1,求解方程组Ax=0的通解形式。
A

B

C
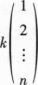
D
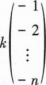
E
使用微信搜索喵呜刷题,轻松应对考试!
答案:
解析:
由题意可知,矩阵A是一个n阶方阵,各行元素之和为零且其秩r(A)=n-1,这意味着矩阵A的列向量中,有一个向量是其余向量的线性组合,即存在某个列向量可以表示为其他列向量的线性组合。因此,对于方程组Ax=0,至少存在一个非零解向量x,使得Ax=0成立。由于矩阵A的秩为n-1,其对应的齐次线性方程组Ax=0必有形如k*[向量]的解(其中k为任意常数),也即通解为参数解形式。因此,选项A正确。
创作类型:
原创
本文链接:给定n阶方阵A,其各行元素之和均为零且r(A)=n-1,求解方程组Ax=0的通解形式。
版权声明:本站点所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明文章出处。让学习像火箭一样快速,微信扫码,获取考试解析、体验刷题服务,开启你的学习加速器!




